学術・語学作品一覧
検索のヒント

![]() 検索のヒント
検索のヒント
■キーワードの変更・再検索
記号を含むキーワードや略称は適切に検索できない場合があります。 略称は正式名称の一部など、異なるキーワードで再検索してみてください。
■ひらがな検索がおすすめ!
ひらがなで入力するとより検索結果に表示されやすくなります。
おすすめ例
まどうし
つまずきやすい例
魔導士
「魔導師」や「魔道士」など、異なる漢字で検索すると結果に表示されない場合があります。
■並び順の変更
人気順や新着順で並び替えると、お探しの作品がより前に表示される場合があります。
■絞り込み検索もおすすめ!
発売状況の「新刊(1ヶ月以内)」にチェックを入れて検索してみてください。
-
5.0◆人はなぜ続けることができないのか? ◆続けるには「信念」が必要だ! 仕事術や成功法、勉強、ダイエットなどなど……人はなぜ続けることができないのか? その答えは「信念」の有無にあります。心の底から信じている「信念」があれば、それは自分を動かすエネルギーとなる一方、外からの借りものであれば、結局何をやっても長続きはしません。では、自分だけの「信念」を見つけることはできるのか? 著者は「信念」を見つける方法として、マインドを記録していく「マインドレコーディング」を提唱しています。本書のテーマ「マインドレコーディング」は、思いつきやひらめきを、自分の原風景と結び付けることで強固な「信念」を得るメソッドです。行動するには理由がいります。その理由になるものが「信念」です。自分を動かすのは「わかっていること」ではなく、「信じていること」です。その「自分だけの理由」である「信念」を本書で一緒に見つけましょう。
-
3.8
-
3.9一般から募った多数の悩みと願望。 「LINE や Facebook に疲れました」 「1年間で100万円貯めたい」 「仕事が山積みなのに現実逃避してしまう」 「心理学でダイエットを成功させてください」 「トークが苦手で、人とうまく雑談できない」 「アガリ症を克服したい」 「好きな人に告白する必勝法を教えて」 「ほしいモノを彼氏に買わせたい」 「働かなくてもいいですか?」 「美人の友人に嫉妬してしまいます」 「六本木で芸能人と友達になりたい」 「浮気を見抜きたい、浮気を予防したい」 etc これらの相談に DaiGo が1分間で答えます。 迷っている時間=止まっている時間。 DaiGo のメンタリズム・アドバイスを聞いて、 まずは行動してみませんか? 明日から何かが変わるはず。 1分間、時間をください。 1分で 「悩み」 を解決、1分で 「不安」 を取り除き、1分で 「苦手」 を克服。 1分で人生は変えられます。 明日が楽しみになります!
-
3.0※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 年収300万円台の家庭で、週3バイトしながら東大に合格! 短期間で偏差値を約20も上げた著者の「実際に効果がある勉強法」といえる、 20の鉄則と28の極意、5つのルールの53の方法を紹介。 1章 なぜ「自宅で勉強」をするべきなのか? 鉄則1 能動的な自宅勉強は、受験だけでなく人生にも役立つ 鉄則2 勉強で時間の「管理能力」「使用能力」を手に入れる 鉄則3 「効率よく思考する」力を身につける 2章 具体的な勉強に入る前に大切なこと 鉄則4 参考書・問題集は各教科1冊ずつに絞る/鉄則5 参考書・問題集は売れているものをチェック 鉄則6 インターネットを使い倒そう/鉄則7 「ルーティン」でエンジンをかける 鉄則8 勉強のノルマを決めよう!/鉄則9 同じタイプの問題を完璧にする布施川式5つのルール 鉄則10 「わからない」でもOK。ただし…/鉄則11 ノートの色はこれだけ。使い方のポイント 鉄則12 自分の活動時間を把握しよう/鉄則13 「勉強時間」「休憩時間」「自由時間」を設定 鉄則14 集中できないときの裏ワザ/鉄則15 すきま時間の使い方は自分で考える 鉄則16 学校の先生を使い倒そう 3章 英語を習得する7つの極意 極意1 英単語は1回にまとまった数ずつ覚える/極意2 ネイティブのマネをしながら発音 極意3 英単語帳は1日に3度見よう/極意4 英文法書は最低3周 極意5 長文読解のコツ 先に問題を確認/極意6 長文読解のコツ 「浮気性」より「一途」に 極意7 英文精読のコツ 「戻り読み」をなくそう 4章 数学の基本は計算力とひらめき 極意1 参考書は分厚いものを選ぼう/極意2 簡単な計算練習を毎日積んで基礎を上げる 極意3 ありがちな計算パターンは覚えておく/極意4 1度目は答えを見ながら解こう 極意5 計算ミスをしたら、なぜ間違ったのか考える/極意6 毎日軽いノルマを決め、それだけは達成 極意7 新しい公式は10回練習 5章 国語は要約力が必要になる 極意1 漢字や語彙をたくさん覚えよう/極意2 図や状況をイメージする 極意3 わからないところは文節で区切りながら音読/極意4 主語と述語をピックアップ 極意5 3回読んでもわからなかったら飛ばす/極意6 文章を要約しよう 極意7 小学生用のドリルから始めよう/極意8 古文は文法をしっかり覚える 極意9 現代語の感覚で覚えないように 6章 暗記系教科は実戦で覚える 極意1 暗記する範囲を絞る/極意2 持っている知識とつなげて、共通点を発見 極意4 知識を定着させるため「3」にこだわろう/極意5 覚えたことは2秒以内に答える 7章 受験のカギは復習法にある 鉄則17 復習するのは「新しく得た情報」「しばらく触れてない情報」 鉄則18 復習でしてはいけないこと/鉄則19 3日以上触れない科目は作らない 鉄則20 過去問と模試を効果的に活用 ほかにも、「教科別の布施川式おすすめ参考書」や「本番で実力を発揮するためのコラム」など、 受験生へのアドバイスが満載。
-
3.8
-
-★★花火と咲いた230人の熱く、切ない珠玉のメッセージ★★ 平安、鎌倉、室町から人気の戦国時代、江戸時代から激動の幕末まで!人生の局面で発したサムライの「1000の言葉}を網羅! 人物像だけではなく、それぞれの夢や悟り、逆境、家族などの各テーマや、家訓、遺言、手紙など写真とともに紹介します! 【目次】 本書の見方 1、萌芽の章 2、激動の章 3、熟成の章 4、変革の章 [参考文献] 特集①人生 特集②こころ 特集③仕事 特集④人間関係 <電子書籍について> ※本電子書籍は同じ書名の出版物を底本とし電子書籍化したものです。 ※本電子書籍は固定型レイアウトタイプの電子書籍です。 ※目次ページでは、該当ページの数字部分をタップしていただくと、すぐのそのページに移動することができます。なお、さくいん並びに本文中に参照ページがある場合及び【立ち読み版】からは移動できませんので、ご注意ください。また閲覧するEPUBビューアによっては正常に動作しない場合があります。 ※本文に記載されている内容は、印刷出版当時の情報に基づき作成されたのものです。 ※印刷出版を電子書籍化するにあたり、電子書籍としては不要な情報を含んでいる場合があります。また、印刷出版とは異なる表記・表現の場合があります。 株式会社西東社/seitosha
-
4.3ラジオの「テレフォン人生相談」で、すでに半世紀近く回答者をつとめてきた加藤諦三氏。その番組の冒頭の言葉は、「あなたの認めたくないものは何ですか? どんなに辛くてもそれを認めれば道は拓けます」である。加藤氏が、ある心理学の先哲の文章を元に考えたものという。本書の内容は、それをどのように実践してゆくかについて、心理学の先哲たちの言葉をひもときながら解説したものである。あらゆる不安、悩み、苦しみに対処するに付いて、前提として持っていなければならない心の在り方を読者に教える。まず、 ◎「人に見せるための生き方」をやめること、そして、 ◎「目の前の現実」から悪い意味で「逃げない」こと、この二つを徹底して心に刻んでゆくレッスンというべき思考トレーニングが展開される。現在の先進国に生きる人々の、「人生観の一般常識」をパラダイムシフトする、驚きの人生論の誕生である。
-
-
-
-「心の貧しい人々は、幸いである。天の国はその人たちのものである」「神の国は、見える形で来ない。神の国はあなたがたの間にあるのだ」本書では、英文学者でありイエズス会の司祭でもある著者が、聖書の中心であるイエス・キリストの福音から70のことばを選び、わかりやすく心をこめて解説する。豊かな時代に生きながらも悩み迷うことの多い私たちに、真の幸福へいたる道を教え示す一冊である。
-
-インド人神父が語る、老後を健やかに生きるための秘訣 平均寿命80歳時代を生きる私たちにとって、定年して会社を退いても人生はまだまだ続きます。そして、人間は歳とともに肉体的には衰えていきますが、最期の瞬間を迎えるまで、精神的には成長することができるのです。本書は、東京・四ツ谷駅近くの聖イグナチオ教会で司祭を務めてきた著者が、「第二の人生を前向きに生きるためにしておくべきこと」をテーマに、長年にわたって講演してきた内容を中心にまとめた一冊。老いを受け入れるための心構え、培ってきた経験を社会に還元していくことの大切さ、老けこまないでいつまでも健やかに生き続けるための秘訣など、限られた時間を存分に生き抜くためのヒントを、神父様がそっと教えてくれます。
-
5.0【自分で自分を幸せにする「透視」】 あなたが自分自身を幸せにする方法、 それが「透視」です。 透視は、決して難しいものではありません。 ちょっとしたコツさえつかめば、誰にでもできます。 そして、透視によって自分の人生を見通し、 幸せな人生を歩むことができるのです。 【大注目のヒーラーによる具体的なレッスン】 「具体的な透視」と口コミで広まり、 経営者、政治家、医師、芸能人からの予約があとを絶たない いま大注目のヒーラーである著者が、 今日からできる10のワークや、 ハイアーセルフとつながる方法、 透視力が上がるオーラの浄化法などを紹介。 【望んだ以上に、現実が動き出す!】 「本当にやりたいことが見つかった」 「クヨクヨしなくなった」 「望んでいた会社で、思ってもみなかったポジションに就けた」 「今まで思いつかなかった仕事のアイデアが、よく湧いてくるようになった」 「イヤなことが起きても、感情が乱れることがとても少なくなった」 「首や肩のコリがラクになり、視界が明るくなって目がよく見えるような感覚になった」 ……など、体験された方から感動の声が続々!
-
4.0すべては映像! 人生、怖いもの知らずでいきましょう。キャメレオン竹田が教える「人生の主導権」を取り戻し、思い通りに生きるヒント なるべく相手の望みを叶えなければという考え、 そうできなかったときの罪悪感、 自分の気持ちを素直に外に出すことへのためらい……。 こうした“モヤモヤ”に心当たりはありませんか? 優しくて繊細な人だからこその悩みですが、 「他人の反応に一喜一憂する人生」には、今日からサヨナラしましょう。 だって、「あなたの世界は、すべて、あなたが創った映像」なのですから! この秘密を知ると、目の前の現実があっさり好転していくんです。 さあ、本書で「人生の種明かし」を始めましょう。――著者 大人気! 著作累計50万部突破のキャメレオン竹田が、 「自分の人生を取り戻し、自由自在に生きるコツ」を伝授します!
-
4.0
-
-「活学」とは、学んだことを知識のみに留めず、知恵として発展させ、実践することである。――今日の変転極まりない社会情勢の中、高い志を持って生き抜くため、我々は今こそ東洋の叡智にその指針を求める必要がある。本書は、『論語』『三国志』『唐詩選』等を通して、東洋学の真髄を現代に活かす方途を語った、滋味あふれる講話録である。物知りは人間の知性の遊戯であり、本質的な値打ちはない。難しい論理や哲学を学んでも、受身による知識の吸収では、生きる力にはならない。自ら主体となって積極的に“深究”して得た知識こそが、生きた学問、すなわち「活学」となる。そうして学んだことは、人間としての立命、情熱、風格、安心となって現れてくる……“東洋学の泰斗”と称えられた著者の、確かな視座からのアドバイスが、心に響く好著である。『活学としての東洋思想』以来、6冊目となる、PHP文庫“安岡活学”シリーズ、待望の完結編。
-
3.0
-
4.0
-
4.0いつ、どんなことが起こっても、マイペースで心おだやかに過ごしたい。 仏教は、そのための“レシピ”なのです。 著作累計100万部の和尚が伝える「自分のこころ」の守り方。 いつも何かに急かされている気がして、ストレスを感じる。 思い切り休みたいけど、のんびりすることに罪悪感がある……。 とかく効率化を重視するのが現代社会。 時にそんな気持ちになったとしても、無理はありません。 しかし、仏教は、心をおだやかにしたいのなら、なるべく「苦」からは脱したほうがいいとします。 お釈迦さまからの「肩の力を抜いて、ホッと一息つけるヒント」を、本書から探してみませんか。 ・あなたを急かしているのは「他人」より「自分自身」かも? ・「急かす人」「自分のペースを乱す人」……ちょっと困ったへの対処法 ・"ほどほど"が一番うまくいく、と仏さまも言っています ・「迷惑をかけ合う」って案外、大事です ・「なるようになる、心配するな!」―― 一休さんの遺言に込められた、深~い意味 ……etc. 「そんな急がなくてもいいんじゃない?」という “心の余裕”が生まれる本。
-
3.7誰もが一度は「人生をやり直したい」と思うもの。夫婦仲が悪い時、成果があげられず、不遇な時、仕事があわないと感じた時。そんな大人の悩みに答えるのが、歴史上の20人の哲学者。ソクラテス、デカルト、カント、サルトル、ニーチェなど、学校の授業で聞いたことのある有名人ばかり。とはいえ、天の声を聞いたのではなく、ご本人も哲学者の肩書きをもつ著者が、彼らの思想、考えを駆使して悩みに答えるという形式。悩みの事例は、著者が主宰する「哲学カフェ」や悩み相談などでよく出てくる人生の難問。たとえば、人間関係の悩み、仕事の悩み、社会への不満、迷いと不安、生きる困難の5つがテーマごとにまとめられている。自分の悩みに重ねて読むもよし、今後の人生で出合うであろう悩みを想像しながら読むもよし。心が張り裂けそうで眠れぬ夜のために……。人生の壁を乗り越え、力強く生きていくための考え方やヒントが見つかるはずだ。
-
-
-
-人生を価値あるものにするのは何か? いま、真の「豊かさ」とは物や環境が手に入ることではなく、「こころの健康」を手に入れることなのではないか、という議論がなされている。 では「こころの健康」とは何か? これまではうつ病などのこころの病気を治せば、その人のこころは健康になると考えられていたが、研究によってこころの病気を治すこととこころの健康を育てることはまったく異なるプロセスであることがわかっている。 本書ではその「こころの健康を育てること」に焦点を当て、こころの健康を構成する5つの要素、(1)ポジティブな感情、(2)エンゲージメント、(3)良好な人間関係、(4)人生の意味、(5)達成感、について、それぞれの意味やそれらを高めるための練習法を紹介する。 練習法ではエクササイズも用意しているので、そこに書き込みながら自分仕様にカスタマイズしていくことにより、自然とこころも健康になっていくだろう。
-
-★先人たちの知恵に学ぶ ★古今東西の知のエッセンス 好評を博している『人生を豊かにする 英語の名言』の第2弾。 著者は「欧州の首都」ブリュッセル在住のビジネスパーソン。「スティーブ・モリヤマ」の筆名でも著書多数。英国勅許会計士およびベルギー王国公認税理士の資格を持つ。 本書は、諺に和訳を付けて並べただけの「英語の諺」集ではない。欧州で長年活躍する日本人ビジネスパーソンの「複眼」から紡ぎ出される、独自の解釈がたっぷり詰まったスーパーエッセイ集。 話題は政治・経済・社会にとどまらない。吃驚仰天の玉手箱。諺に絡めた摩訶不思議な「ショートショート」4篇も収録。
-
3.0著者は欧州ブリュッセル在住で、世界最大の国際会計事務所プライスウォーターハウス・クーパースの重役職にある現役ビジネスマン。取得した難関資格は数知れず。本書ではヨーロッパ流の「勝ち組」の条件を始めとして、人生の機微を偉人たちのコトバを通して、含蓄あるエッセイで語りきる。取り上げた名言は、5000を超える名言のなかから特にわれわれ日本人の心に沁みる傑作を著者が3年を掛けてセレクトしたもの。どこからでも読める見開き2頁構成で、用途に合わせて読めるように8つのジャンルに分けた。暗唱して、挨拶・スピーチで使うと効果てきめんの名作ぞろい。特に管理職層の方々にお勧めの一冊である。欧州トヨタ自動車社長兼CEOの豊田周平氏絶賛!
-
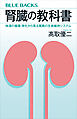
4.0日本人の2000万人以上、成人の5人に1人が「慢性腎臓病」といわれる現代に必読の一冊。 腎臓は握り拳ほどの大きさで、左右に2つあり、その重さはたった150グラムほどの臓器です。 1日に150から180リットルの体液を濾過し、水分・ミネラル・pHを調整する驚きの生命維持装置「腎臓」 365日24時間休むことなく老廃物の除去し、体液をとおして体の各器官のはたらきを調整しているこの臓器は、30代をピークに減少し、再生することはありません。60歳を過ぎると腎臓は1年で16立方センチメートル減少するといわれています。 人生100年時代に、自分の腎臓で健康に生きるためには? その基礎から最新の医療情報までをお届けします。 再生医療でもっとも実現が難しいといわれるその精緻な構造と老廃物を除去する巧妙なしくみ、神経ネットワークや内分泌ネットワークを介して行われている脳や腸、心臓といった全身の器官との連携についてを中学・高校理科の知識をもとにやさしく解説します。また、なぜそのような複雑なメカニズムを獲得したのか、その理由を生命38億年における進化史から紹介。 さらに、慢性腎臓病約2000万人という時代に知っておきたい、現代人のための正しい医療知識や食事の注意点や運動法といった生活習慣による腎機能維持の方法までを、書籍やテレビ番組でも知られる腎臓専門医・髙取優二先生ががていねいに解説します。
-
3.0
-
-腎機能をキープ! 身体への負担も少ない腹膜透析のはじめ方 趣味や仕事も続けられる! 人生を諦めない!! 充実した生活を守る最強の療法 ・導入の手術は30分 ・血液透析よりも少なくなる通院回数 ・腹膜透析患者の生活パターン ・食事制限もゆるやか 患者さんの不安や疑問に答える一冊! 「医者から『そろそろ透析です』と言われた」人や、「いま透析しているがとてもつらい」、「ほかの透析方法、病院はないのかと探している」方に知ってもらいたい、「腹膜透析」。施術回数が少なく、自宅や外出先、旅行先でも受けられ、食事制限も少ない「腹膜透析」の治療やメリットを泌尿器科の医師が紹介する透析治療ガイド。 【目次】 はじめに 第1部 これだけ知っていればOK! 腎臓病と透析の基礎知識 第2部 PART1 腹膜透析をしながら充実した人生を送るには 第2部 PART2 PD早わかりQ&A おわりに 巻末付録 PD最新情報
-
-「人工透析は避けたい」という願いを叶えるために! 「腎臓を守ると、動脈硬化を抑制して寿命を永らえることができる」ことが分かってきました。現在健康な人にとっても、長寿につながる情報満載です。 患者さんの心強い味方、臨床研修医の病態把握に。看護師さん・栄養士さん・薬剤師さんの患者指導にも役立つ本。 ◆著者は腎臓病治療30年以上のエキスパート 岩崎滋樹医師は、腎臓内科一筋30年以上の臨床経験を持ち、進歩著しい腎臓病治療の第一線で臨床のかたわら、手間のかかる食事療法を医療に組み込む一方、患者さん向けの講習会で好評を博しています。 横浜市立市民病院 腎臓内科 部長 昭和大学医学部 腎臓内科学 客員教授 慶応義塾大学医学部 客員講師 ◆視覚的に直感的に理解できる 腎臓の働き、腎不全の病態変化、治療のポイントがテンポよく解説されています。 イラスト、表、グラフ 100 点以上を用い、直感的に理解できます。 腎臓病は、食事などの生活習慣を改善することが非常に大切です。本書は、30年以上腎臓病治療に精魂傾けてきた腎臓病専門医の岩崎滋樹医師が、これだけは押さえてほしいと痛感したポイントを厳選して掲載しています。 ◆腎臓病は新たな国民病 慢性の腎臓病患者さんも、推定1,330万人で、日本人の1割以上を占めています。 治療が必要とされる患者さんだけでも約600万人と推測されており、その数の多さから「新たな国民病」とも言われています。 ◆腎臓を守ることは寿命を伸ばす 腎臓を守ることで、動脈硬化を抑制して寿命を永らえることができます。 また、腎臓は他の臓器同様、加齢により機能低下していきます。もともと腎臓が弱くないと思っていた方々も、寿命100歳時代を見越して、腎臓の保全に心がけていくことは大切です。
-
4.0※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 失われた人体や臓器を丸ごと再生することは、まだできない。しかし、傷ついた組織や臓器を修復することで、失われた機能の再建はできる。脊髄損傷によるマヒや、心不全、角膜損傷、網膜の障害、難聴など、これまで治療不可能とされてきた障害も、細胞の移植やロボット技術の開発などで、克服できる可能性が出てきた。iPS細胞など最新の研究内容も織り交ぜて、再生医療の最前線をお伝えする。(ブルーバックス・2010年9月刊)
-
4.0生命科学の現場を世界各地で徹底取材。 医学と人体の常識を覆す1冊! すべての細胞がメッセージを出し合うことで、 私たちの生命は維持されている―― この人体観は、最先端の中の最先端です。 ――山中伸弥(京都大学iPS細胞研究所所長) いま、生命科学の進歩により、「脳を頂点とするピラミッド」という人体観が覆されようとしている。臓器同士のメッセージのやりとりが、私たちの体を支えるカギとなっていることがわかってきたのだ。人体はどのように成り立っているのか? そもそも、病気とは何か? 健康長寿を実現するためには何が必要なのか? 最先端の医療現場への取材から得られた知見を基に、新たな人体の姿を描く!
-
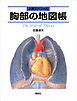
-※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 【胸にある器官はどこからきたのか?】 心臓、肺、食道、横隔膜、乳腺、胸腺、胸壁の筋と骨の構造となりたちを探る。 胸にある臓器の多くは、遠く首から降りてくる神経によって支配されている。 その事実にこそ胸部器官のなりたちの不思議が秘められている。 《本書のおもな内容》 ●総論――ヒトの心臓はなぜ胸部にあるのか/サメとヒトの心臓をくらべる/胸部とはどのような場所か/胸壁を形づくる筋 ●心臓――大血管と心臓/心臓を養う冠状動脈/心臓の静脈/心臓の4つの部屋――心房と心室/2心房2心室ができるまで/心臓の血液循環――出生前と出生後/4つの弁のつくりと開閉のしくみ/弁音をどこで聴くか/心臓を動かすしくみ/心臓の自律神経/心臓を二重に包む心膜 ●肺――拡張と収縮をくりかえす肺/空気の通り道――気管と気管支/肺区域とはなにか/肺門と肺根とは/肺の内部を走行する動脈と静脈/肺の自律神経/肺のリンパの流れかた/肺を二重に包む胸膜 ●食道――頸・胸・腹部の3領域にまたがる食道/食道が狭くなる場所/食道壁の3層構成/食道の動脈と静脈/食道の自律神経 ●横隔膜――横隔膜とはどのような膜か/横隔膜のつくりと形/横隔膜のウィークポイントと横隔膜ヘルニア/横隔神経はどこからくるのか ●乳腺――乳房を形づくるもの/乳腺はどこにできるのか/乳腺を包む膜/乳腺のリンパの流れかた/乳頭のつくり ●胸腺――胸腺とはどのような器官か/乳児と大人の胸腺のちがい/胸腺を養う2系統の動脈 ●胸壁と胸郭――胸壁をつくる骨と筋/胸壁の浅層に位置する大胸筋、小胸筋、前鋸筋/胸壁の深層に位置する肋間筋/胸壁の筋ができるまで/肋間神経とはどのような神経か/胸郭を動かす関節/呼吸運動による胸郭の変化 ※この商品は紙の書籍のページを画像にした電子書籍です。文字だけを拡大することはできませんので、タブレットサイズの端末での閲読を推奨します。また、文字列のハイライトや検索、辞書の参照、引用などの機能も使用できません。
-
-※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 《講談社 地図帳シリーズ》 【ヒトの脳は、なぜ巨大化し、複雑になったのか?】 脳の形態の変遷をみきわめれば、脳がもつ機能が自然にみえてくる 《本書のおもな内容》 【総論】 【下位脳】 脊髄/脳幹/小脳 【上位脳】 間脳/終脳 【脳室、髄膜、血管系】 脳室/脈絡叢/脳脊髄液/髄膜/血管系 【図譜でみる脳の内部】 脳幹の内部/間脳と終脳の内部 《なぜ神経解剖学の理解が大切か?》 神経学の診断はきわめて理論的である。ある意味で、 数字の計算や問題を解くのとよく似ているといえるであろう。 その神経学の診断の基礎となるのが、神経解剖学である。 脳と脊髄からなる中枢神経系は、種々のはたらきをもつ 中枢や脳に区分され、これらの明確な機能を果たす中枢間 には相互に連絡する線維路が形成される。特有な機能をもつ 中枢と、それが存在する場所、さらにここに出入りする神経線維 の経路(これを伝導路とよぶ)は、たとえていえば数学の公式や 定理に相当するといってもよいであろう。公式や定理なくして 正しい解答は導きだせないように、神経解剖学の理解なくして 正しい判断はくだせない。これはきわめて大切なことと理解して いただけると思う。 (本文「総合案内」より) ※この商品は紙の書籍のページを画像にした電子書籍です。文字だけを拡大することはできませんので、タブレットサイズの端末での閲読を推奨します。また、文字列のハイライトや検索、辞書の参照、引用などの機能も使用できません。
-
5.0※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 【内容紹介】 「なんで血は赤いんだろう?」、「骨は全部でいくつあるんだろう?」、「なんでうんちはくさいんだろう?」、「なんで鼻をつまむと変な声になるんだろう?」と、思ったことはありませんか? この本は、そんな体についてのしつもんの答えを、楽しい絵でおぼえる図鑑です。 (本文はすべてルビあり) 【著者紹介】 [絵]つぼいひろき 東京都生まれ。プロボクサー、印刷会社営業を経てイラストレーターに。ユーモアのあるイラストで世の中に(笑)をつけるお仕事をしています。著書:『いえでおふろ』(教育画劇)、『いたいのいたいのとんで研究所』(三恵社)、『なやみとーる③転校生のなやみ』(岩崎書店)/イラスト担当本:『おぱんつロック ウンチョス大とうりょうのたんじょうび会だぜ!』(主婦の友社)、『超爆笑100連発! お笑い天国』(ポプラ社)など。 [文]ペズル 編集ライター。著書:『もしも虫と話せたら』、『もしもカメと話せたら』、『もしも鳥と話せたら』、『もしも恐竜と話せたら』(プレジデント社)、『366日のにゃん言葉』、『366日の美しい昆虫』、『物語のある鉱物図鑑』(三才ブックス)など。 [監修]三枝 慶一郎(さえぐさ・けいいちろう) 医師・医学博士。都内総合病院に消化器内科医として勤務。専門は潰瘍性大腸炎やクローン病などの炎症性腸疾患。 【目次抜粋】 【1時間目】食べ物の流れ 1 味はどこで感じるの? 2 なんでよくかんで食べないといけないの? 3 のどちんこってなんであるの? 4 胃は何をするところ? 5 胃はどれくらい大きいの? …… 【2時間目】血の流れ 16 血はどこで生まれるの? 17 体に血が流れているのはなんのため? 18 なんで血は赤いの? 19 血管ってどれくらい太いの? 20 心臓は1日に何回ドクドクするの? …… 【3時間目】情報を感じる 29 なんで悲しいとなみだが出るの? 30 なんで人間はまばたきをするの? 31 グルグル回転すると目が回るのはなぜ? 32 動画でとった自分の声がなんか変に聞こえるのはなぜ? 33 鼻毛はなんであるの? …… 【4時間目】体を動かす 40 骨は全部でいくつあるの? 41 一番大きな骨はどれくらい? 42 なんで子どもは背がのびるの? 43 筋肉って何? 44 なんでおとなは肩がこるの? …… 【5時間目】そぼくなぎもん 49 つめって何でできているの? 50 なんで頭にだけ毛がたくさんあるの? 51 かみの毛は1か月でどれくらいのびるの? 52 つばってなんのためにあるの? 53 なんで子どもの歯はぬけちゃうの? ……
-
-わずか1万円の遺伝子レベルの検査で、将来、自分がかかる病気がわかるとしたら、あなたはどうしますか? 乳がんリスクのために、乳房を二つとも切除したことを発表した女優のアンジェリーナ・ジョリーのニュースは、遺伝子検査時代の到来を世界に知らしめた。 ■エイズにならないための遺伝子を特許申請 ■ぜん息の遺伝子が特許として認められた ■ヒトの遺伝子が次々と特許の対象に ■各種のがんや生活習慣病、嗜好まで「特許」の対象に ■山中伸弥教授のiPS細胞をめぐり特許争奪戦勃発 子どもの知的能力や芸術、運動能力を占う企業も上海に誕生した。ますます激化する遺伝子ビジネスで、人体にかかわる物質すべてが特許戦争の波の中へ。NHKスペシャル「人体特許」のプロデューサーが、その後の調査を経て書き下ろす。
-
-【ご注意】※この電子書籍は紙の本のイメージで作成されており、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。お手持ちの端末で立ち読みファイルをご確認いただくことをお勧めします。 不思議な人体の世界に入ってみよう! 天才発明家のじいちゃんによって開発された縮小マシンに乗って、人体の謎を探るべく、孫の大介、幼なじみの沙英たちは、じいちゃんの弟子・ミコトの頭部に潜入! この本では特に、眼、耳、口、鼻、脳を取り上げて解説します。見る、聞く、食べる、匂いをかぐ、息をする、考える…私たちが当たり前のように行っていることも、人体の不思議な機能が働いているからこそできること。 さあ、みなさんもまんがの登場人物たちと一緒に、人体の世界を冒険してみましょう。きっと新たな発見や驚きがあるはずです。 ※この作品はカラー版です。
-
3.3※この電子書籍は固定レイアウト型で配信されております。固定レイアウト型は文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 人間はどこまで耐えられるのか? 人間の能力はどこまで伸ばせるのか? 生理学、心理学、運動学、生物学、物理学、化学、栄養学などの観点から、人体の限界を図解イラストで解説。 人体の限界を知り、健康的な生活を送るための画期的な科学教養書。
-
-※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 「健康づくりのための身体活動・運動ガイド 2023」など最新の知見をふまえ、フルカラー化して改訂。高齢者の運動生理の充実や、運動療法の見直しなど特定保健指導や健康運動指導士取得に必須。 ※この商品は紙の書籍のページを画像にした電子書籍です。文字だけを拡大することはできませんので、タブレットサイズの端末での閲読を推奨します。また、文字列のハイライトや検索、辞書の参照、引用などの機能も使用できません。
-
-※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 消化器系や循環器系を詳しく学び、代謝を学ぶ生化学につなげる。専門科目の臨床栄養学や発達・成長に必要な栄養学、食物アレルギーや誤嚥の理解に必要な基礎知識を幅広く取り上げた。カラーイラストを多用した見てわかる構成に。 【シリーズ総編集】 木戸 康博(金沢学院大学人間健康学部 教授) 宮本 賢一(徳島大学大学院医歯薬学研究部 教授) 【シリーズ編集委員】 河田 光博(佛教大学保健医療技術学部 教授) 桑波田雅士(京都府立大学大学院生命環境科学研究科 教授) 郡 俊之(甲南女子大学医療栄養学部 准教授) 塚原 丘美(名古屋学芸大学管理栄養学部 教授) 渡邊 浩幸(高知県立大学健康栄養学部 教授) 【編者】 河田 光博(佛教大学保健医療技術学部 教授) 小澤 一史(日本医科大学大学院医学研究科解剖学・神経生物学分野 大学院教授) 上田 陽一(産業医科大学医学部第1生理学 教授) 【執筆者一覧】 上田 陽一(産業医科大学医学部第1生理学 教授) 大島 勇人(新潟大学大学院医歯学総合研究科硬組織形態学分野 教授) 小澤 一史(日本医科大学大学院医学研究科解剖学・神経生物学分野 大学院教授) 小野 克重(大分大学医学部病態生理学講座 教授) 影山 晴秋(桐生大学医療保健学部栄養学科 教授) 上條義一郎(和歌山県立医科大学リハビリテーション医学講座 准教授) 河田 光博(佛教大学保健医療技術学部 教授) 林 泰資(ノートルダム清心女子大学人間生活学部食品栄養学科 教授) 樋口 桂(文京学院大学保健医療技術学部理学療法学科 教授) 松﨑 利行(群馬大学大学院医学系研究科生体構造学分野 教授) 三浦公志郎(九州女子大学家政学部栄養学科 教授) 宮坂 京子(社団法人日本リウマチ研究所 理事) ※この商品は紙の書籍のページを画像にした電子書籍です。文字だけを拡大することはできませんので、タブレットサイズの端末での閲読を推奨します。また、文字列のハイライトや検索、辞書の参照、引用などの機能も使用できません。
-
-※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 ロングセラー『生化学』待望のフルカラー化。 好評の簡単明瞭な記述とビジュアルな構成はそのままに、最新情報に更新。 管理栄養士国家試験のガイドラインに準拠。 先生と学生をつなぐテキスト ※この商品は紙の書籍のページを画像にした電子書籍です。文字だけを拡大することはできませんので、タブレットサイズの端末での閲読を推奨します。また、文字列のハイライトや検索、辞書の参照、引用などの機能も使用できません。
-
-
-
-※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 栄養学を学ぶために必要な人体の構造と機能を、簡潔明瞭にまとめた好評テキストのフルカラー改訂版!生化学、栄養学総論、臨床栄養学へつながる基本的な知識を効率よく学べる。 【シリーズ総編集】 木戸 康博(金沢学院大学人間健康学部 教授) 宮本 賢一(徳島大学大学院医歯薬学研究部 教授) 【シリーズ編集委員】 河田 光博(佛教大学保健医療技術学部 教授) 桑波田雅士(京都府立大学大学院生命環境科学研究科 教授) 郡 俊之(甲南女子大学医療栄養学部 准教授) 塚原 丘美(名古屋学芸大学管理栄養学部 教授) 渡邊 浩幸(高知県立大学健康栄養学部 教授) 【編者】 河田 光博(佛教大学保健医療技術学部 教授) 三木 健寿(奈良女子大学 名誉教授) 鷹股 亮(奈良女子大学研究院生活環境科学系生活健康学領域 教授) 【執筆者一覧】 上田 秀一(獨協医科大学解剖学(組織) 教授) 小澤 一史(日本医科大学大学院医学研究科解剖学・神経生物学分野 教授) 椛 秀人(高知大学医学部医学科生理学講座 特任教授) 河田 光博(佛教大学保健医療技術学部 教授) 坂本 浩隆(岡山大学理学部付属臨海実験所 准教授) 紫藤 治(島根大学医学部環境生理学 教授) 千田 隆夫(岐阜大学大学院医学系研究科病態制御学講座 解剖学分野 教授) 高野 康夫(高知リハビリテーション専門職大学リハビリテーション学部 教授) 鷹股 亮(奈良女子大学研究院生活環境科学系生活健康学領域 教授) 中島 昭(松山東雲短期大学 名誉教授) 西 真弓(奈良県立医科大学医学部医学科第一解剖学 教授) 能勢 博(信州大学医学部 特任教授) 三木 健寿(奈良女子大学 名誉教授) 村松 陽治(関西福祉科学大学健康福祉学部福祉栄養学科 教授) 森 千里(千葉大学大学院医学研究院環境生命医学 教授) 森田 規之(安田女子大学家政学部管理栄養学科 准教授) 由利 和也(高知大学医学部医学科解剖学講座 教授) 依田 珠江(獨協大学国際教養学部言語文化学科 教授) ※この商品は紙の書籍のページを画像にした電子書籍です。文字だけを拡大することはできませんので、タブレットサイズの端末での閲読を推奨します。また、文字列のハイライトや検索、辞書の参照、引用などの機能も使用できません。
-
-※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 ナショナル ジオグラフィックの定番、人気ジャンルの一つ、「科学」の中でも、とりわけDNAや脳、生死など“人体”にかかわるテーマにフォーカスした別冊です。 研究の最前線に立つ人たちに取材し、フィールドにも足を運んで人々の声を聞き、ナショジオならではの生の情報を、豊富なビジュアルとともにお伝えします。 ※本書は、『ナショナル ジオグラフィック日本版』に掲載した特集を再録したものです。
-
-
-
3.8《とんでもなく複雑で、とんでもなく精巧──内なる秘境、人体。さあ“秘密の人体”へ分け入る旅へ!》 私たちの未来に最もインパクトを与えるのは、自動運転車でもロボットでもない。 ――「ヒト生物学」だ。 ---------------------- 私たち自身の体内に広がる「ミクロの宇宙」。 知るためには、まず、見なければならない。 それぞれの時代時代で、研究によって得られた知識をもとに私たちは自らの体を「見て」、そして考えてきた。そこには、人体を見ようと奮闘した科学者たちの物語があった。その営みは今も脈々と続いている。 ---------------------- 新たなテクノロジーとツールによって明かされてきた人体の姿は、息を呑むほど精巧で、複雑で、多様性に溢れている。その光景は私たちに問いかける。 細胞とは何なのか、何をもって健康とするのか、そして、生命とは何か──。 「ヒト生物学」における近年の画期的発見の数々は、私たちの人生をいかに変えたのか。前著『美しき免疫の力』で優れたストーリーテラーぶりを披露し、英国で最先端の顕微鏡を用いて免疫細胞を研究するダニエル・M・デイヴィスによる、ヒト生物学の最前線。 ---------------------- 【目次】 ■科学者のみなさまへ ■はじめに ■一章……超高分解能で細胞を見る──顕微鏡の発展とともに ■二章……命の始まり──遺伝子検査とゲノム編集 ■三章……新しい治療法を生むテクノロジーの力──フローサイトメーター ■四章……色鮮やかに脳を染める──多色標識法と光遺伝学 ■五章……内なる他者との共生──マイクロバイオーム ■六章……包括的な遺伝コード──ホリスティックな医療へ ■七章……全体を見る ■謝辞 ■訳者あとがき ■原註 ■索引
-
4.0膵臓がんを主たる専門とする外科医として多くの実績をあげてきた著者が、人体について、細胞のふるまいから臓器の働き、老化やがん、免疫といった現象までを易しく解説します。細胞内の現象、生体内の現象、ヒト社会の現象、それらはすべて、内界と外界とのコミュニケーションから成り立っています。これらの巧妙な仕組みを、それぞれのレベルで対比して考えてみると、どのレベルの世界にも同じような社会現象があるということがわかって面白いものです。実社会の事象や人物、物事、音楽・映画作品などへの喩えや関連するエピソードをふんだんに交えながら展開される「人体」の話は深く、興味深く、読者をその世界へと導きます。専門知識を持たない方でも肩肘張らずにスッと入れる“通読できる”人体の教科書です。
-
-※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 シリーズ累計500万部を超える大人気「動く図鑑MOVE」シリーズのポケットサイズ図鑑、「MOVE mini」に、近年世界中で関心が高まっている「人体」が新登場! ●主な内容 美しい見開きイラストで全身を巡っていく構成。まるで人体の中を小さくなって探検しているような図鑑です。 骨格・筋肉から、脳のしくみ、胎児の成長、ips細胞まで。そのほか、近年明らかになってきた伝達物質。私たちの体のメカニズムを美麗イラストや電子顕微鏡写真を用いて詳細に解説。そのほかに、医学の歴史や、最新医療についても触れる。 ■MOVE mini『人体のふしぎ』の特徴 1.ダイナミックで美しいイラストと、最新の顕微鏡写真が満載! 美しい見開きイラストで全身を巡って構成は驚きの連続! まるで人体の中を小さくなって探検しているような気持ちで、子どもも大人も楽しめる。NHKスペシャル「人体」からの画像も満載! 2.電子顕微鏡による貴重な写真を豊富に使用! 60兆個の細胞でつくられ、2000億個のニューロンによって動かされ、 ときに目では見えない0.01mmほどの小さな細胞に助けられる、わたしたちの人体。 電子顕微鏡を用い、巨大すぎるミクロワールドにせまります。 3.はじめて科学や人体のふしぎに触れる子どもにもおすすめ! 大人の学び直しにも! 人体や医学に関する専門用語もできるかぎりわかりやすく紹介! 人体について「知りたい」が すべて詰め込まれています。 ※この商品は紙の書籍のページを画像にした電子書籍です。文字だけを拡大することはできませんので、タブレットサイズの端末での閲読を推奨します。また、文字列のハイライトや検索、辞書の参照、引用などの機能も使用できません。
-
3.8〈クリニックを開業するのは、患者さんたちの身体といっしょに人生の風景を眺める、冒険旅行になぞらえられるかもしれない。よく知っている地形に見えても、往々にして分け入った小道が開けて、日々新たなパノラマをのぞくことになるのだ〉ルネサンス期、魂がどこよりも近くにあると考えられていたのが、唇だった。形を変えただけで息が温かくなったり冷たくなったりするのが、生命力の証拠だと思われていたのだ。また一七世紀の天文学者たちは、星の見え方をもっとよく知るために、目の構造に注目した。私たちの身体は、いつでも世界を知るための冒険の入り口だったのだ。スコットランドの総合診療医フランシスは、ときに救急医や従軍医として、さまざまな患者を診てきた。顔半分だけが麻痺した女性、手のひらを釘で打ち抜いた大工、直腸にケチャップの瓶が入った男性……。本書はそんな患者たちとフランシス、そして人体の解明に挑んだ偉人たちの冒険の物語だ。小説のような文体に人体をめぐる薀蓄を交えた、「読む人体図鑑」とも呼べるノンフィクション。さあ、人体をめぐる旅に出よう。
-
-人体とは、私たちヒトにとっては最も身近でありながらその働きに最も疎い、いわば探検しつくされた世界に残る最後の「未踏の地」である。新しい器官が発見され、各種テクノロジーでその限界が拡張されつつある人体はいわば、貪欲に版図を広げる「帝国」なのだ! その人体をテーマに、名画を解説するように、専門文献から絵画、文学、各種エンターテインメントからの引用を縦横に駆使し、ドライなユーモアとウィットをふんだんに盛り込んだ文章で科学的な事柄を解説する名キュレーター、オールダシー=ウィリアムズが、実際に解剖されつつある人体にも取材し、探索と発見の旅の顛末を語る「人体読本」。
-
-※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 ※この電子書籍は紙版書籍のページデザインで制作した固定レイアウトです。 「とにかくわかりやすい!」だけじゃなく、ワクワクしながら読める! 私たち自身の「からだ」は、私たちにとって最も身近な存在であるにもかかわらず、わからないことがたくさんあります。臓器のはたらきやそのしくみについて知れば、これまで以上に自分のからだについて関心をもち、健康維持に意識を向けられるはずです。 本書では、人体をつくっている骨や筋肉、臓器を取り上げ、その基本的なはたらきを解説するとともに、普段は意識しないような「すごい」機能を紹介します。「どうして病気になるのか」「医療機器はどう使われているのか」「どんな生活が健康的か」など、気になるテーマも盛り込まれています。医療系の専攻でなくても、興味さえあれば気軽に読める一冊です。 〈こんな方におすすめ〉 ◎人体の仕組みや自身の健康に関心がある人 ◎医療職や生物系の学問に興味がある中高生 ○人体について子どもに教えたい保護者・教員 はじめに/目次 Chapter 1 人体の成り立ち 1. 骨はパイプや軽石のように軽くて丈夫 2. 骨と骨のつなぎ目には動かないものがある 3. 肘を曲げると「力こぶ」ができるのはなぜ? 4. 赤筋と白筋の割合で得意なスポーツがわかる! 5. 舌は骨格筋のかたまり 味を感じるだけじゃない! 6. マルチタレントな臓器、肝臓 コラム 肛門は単なる便の出口ではない! 7. 喉頭は気流を利用した発声器 8. 気管と気管支は「自動清浄機能付きの真空掃除機」 9. 尿は体内で不要な物質が溶けたもの 10. 膀胱が十分にふくらまないと頻尿に? 11. 精巣は暑がり 暖め過ぎると不妊症に? 12. 排卵は月1回、左右の卵巣からランダムに起こる! 13. 眼はオートフォーカスの高性能カメラ 14. 音を聴くだけではない耳のはたらき Chapter 2 ここがすごい! からだを維持する機能 15. すべての情報は脳につながる 16. 脳のどこで「記憶」されるの? 17. 小脳がスムーズなからだの動きを司る 18. 命が宿る脳幹の大きさは小指1本分!? 19. 食欲を調節する摂食中枢と満腹中枢 20. 言葉を司る二つの言語中枢 21. 神経は「電気が流れる電線」 22. 親指が人類に文明をもたらした!? 23. 体温や水分量を一定に保つホメオスタシス 24. 生まれる前から死ぬまではたらき続ける心臓 25. 心臓の働きを時々刻々調節する自律神経 26. 脳に血液を確実に送るしくみ、大脳動脈輪 27. 血液には出血を抑えるはたらきがある 28. 細菌やウイルスに対する抗体を含む血液 29. リンパ管は体内の排水路 30. 脳を守る髄液 31. からだのエネルギー源、ATP 32. カルシウムは骨を硬くするだけではない! 33. 酸素の運び屋、ヘモグロビン 34. 微量でも効果絶大なホルモン Chapter 3 どうして? からだの変化や反応のしくみ 35. 太りやすい人と太りにくい人の違いは? 36. まぶしいときに目が閉じてしまうのはなぜ? 37. 赤ちゃんはなぜ体温が高い? 38. 毛はどのように生え変わる? コラム 毛が生えるところと生えないところ 禿げるのはなぜ? 39. アレルギーは何が起きている? 40. 傷はどう治るの? 41. 「遺伝」って何? 42. カフェインで目がさえるのはなぜ? 43. お酒を飲むとトイレの回数が増えるのはなぜ? 44. 男性・女性に分かれるのはいつ? 45. どうしていびきをかくの? 46. 寝ているときにみる「夢」ってなんだろう? コラム 気になる思春期の変化「声変わり」 Chapter 4 なぜ、人は病気になるの? 47. 頭痛にはどんな種類がある? 48 .めまいはなぜ起こる? 49. うつ病ってどんな病気? 50. 感染症では体内で何が起こっている? 51. なぜ、がんになるの? 52. 心筋梗塞はどうして起こる? 53. 糖尿病の原因は甘いものの食べ過ぎ? 54. 病気に遺伝は関係するの? 55. 白内障と緑内障の違いは? 56. ギックリ腰ってどこを痛めているの? Chapter 5 気になる! 医療のあれこれ 57. なぜ麻酔をかけると痛くない? 58. 人工心肺はどんなときに使われる? 59. レントゲンで体内を撮影するしくみ 60. からだの断面図を見ることができるMRI検査 61. 視力を矯正するレーシック手術とICL(眼内コンタクトレンズ) 62. 血液検査でがんがわかる? 63. 血圧を正確に測るためには 64. 便に血が混じったら異常? 65. 一緒に飲むとよくない薬の飲み合わせとは? Chapter 6 人体に関する迷信のウソ・ホント 66. 食べてすぐ横になると「牛になる」ってホント? 67. 乾布摩擦はホントに健康に良い? 68. 笑うと健康に良いのはホント? 69. ワカメを食べると髪が増えるのはホント? 70. 毛を剃ると濃くなる? 坊主にするとくせ毛になりやすい? 71. テレビを見すぎると目が悪くなるのはホント? 72. しゃっくりを止める方法があるのはホント? 73. 耳がツーンとしたときの解消法があるのはホント? 74. 鼻血が出たら上を向くべきなのはホント? Chapter 7 健康のために知りたい日常の知識 75. 「朝活」はからだに良い? 76. からだのために良い食事は? 77. たばこはからだにどう影響する? 78. 適切な飲酒量は? コラム 音楽による健康効果 79. 1日何歩歩くと健康に良い? 80. 運動前の準備運動の効果は? 81. 日光を浴びるのは健康に良い? 82. 熱があるときの入浴はNG? 索引
-
5.0
-
-『[神代文字]言霊治癒のしくみ1&2』に続くNEW HEALING WAVE 第3弾! 神代文字最高エネルギー「ホメミ文字」のほか「カタカムナ文字」「龍体文字」「ホツマ文字」「フトマニ」を使った治癒体系の全貌! 『なぞる本 神代文字練習帳』『超パワー結界モデル ホツマふとまにカード128ピッコロ』『なぜか病い・不調が癒える 神代文字&呪文カード』も同時発売! 本書は日本の古代文字、古文献、古神道に隠されていた優れた治療法の実体を豊富な事例とともに治療の現場から惜しげもなく公開したかつてない画期的な情報である。 ・ホツマ文献(「ホツマツタヱ」や「フトマニ」など)と神道の祝詞をカタカムナ文字で解釈していくことを試みたら、古代日本の治療法と健康法が見つかった ・大和ことばの中に組み込まれた《治癒情報》 ・からだのなまえに秘められた《治癒情報》 ・カムロギ・カムロミの渦の気功治療 ・神代文字を使った気功治療 古代の天皇を「スメラミコト」といいますが、それは、一般の人が見えない物に対して「見える眼をもっている人」という意味です。 神代文字を使った気功治療は、音霊(オトダマ)、形霊(カタダマ)として、空間の素粒子を人体に取り込んでいき、作用しています。 これほど優れた言葉と文字を持つ民族はいません。 ・神代文字は文字がもつ固有の振動数の効果によって作用が違います ・霊界クサ文字を毎日書いていると、顔がだんだんきれいになっていく ・ホメミ文字のひふみ祝詞は10の94乗の波長を出している ・皮膚にホツマ文字や龍体文字を描くと、筋肉の痛みが瞬時に消え、不調が解消します ・ありがとう曼荼羅で天の気、地の気が整い、病気の予防になります ・病気封印の結界ストーンサークルと呪文を大公開 ・龍体文字×あわ歌(骨、北) ・ホメミ文字×ひふみ祝詞(腎・膀胱、北東) ・ホメミ文字×あわ歌(胆・肝、東) ・カタカムナ文字×ひふみ祝詞(皮膚、南東) ・カタカムナ文字×あわ歌(脾・胃、南) ・龍体文字×ひふみ祝詞(肺・大腸、南西) ・ホメミ文字×ひふみ祝詞(筋肉・腱、西) ・ホツマ文字×あわ歌(心臓・小腸、北西) ・ホツマ文字×ひふみ祝詞(神経、上方) ・カタカムナ文字×あわ歌(靭帯、下方) 実践して楽しむ片野式古代文字パワー活用のためのアイテムが勢ぞろい!『神代文字で治療師になる』『なぞる本 神代文字練習帳』『ホツマふとまにカード128ピッコロ』『神代文字&呪文カード』『神代文字ヒーリングパワー自動充電三角シート』が同時発売中!
-
3.7漢字伝来以前から日本にあったとされる神代文字。近世に作られたそれらの文字と文献には神道や和歌をめぐる多様な知が集積している。その一つ、ホツマ文献にその集積を探る。
-
4.0山本光輝が神代文字を 揮毫(きごう)すると「祝詞・護符」のチカラに! 言葉の現象化の法則がついに明らかとなる! 現実創造の神秘的メカニズムを神代文字を通して解き明かす驚天動地の書! 祈りや想いの現象化に対してようやく科学のメが入った! 「山本光輝の書は、神の姿を拓しだす『神拓の書』だ」(保江邦夫理学博士) 言霊の幸わう国日本と日本人の特殊性に迫る! 「山本光輝が『神代文字』を揮毫(ルビ:きごう)するとなぜ、『護符』の効力を発揮するのか」 言葉が神であることを人類は忘れてしまった 宇宙意志なる神のお手伝いは神代文字を通して可能になる その方法はこの本にすべて書かれている
-
5.0事物が存在するということは、それが知覚されているということである──。ジョン・ロックの経験論哲学の批判的継承者たるジョージ・バークリー(1685-1753)は本書『人知原理論』において、こう断言する。それは裏返せば、知覚されないものは存在しない、つまり私たちの心から切り離された「物質」なるものなど存在しない、ということだ。様々な批判にさらされながらも、ヒュームやカント、ドイツ観念論など後の哲学思想に多大な影響を与えたバークリーの思想とはいかなるものか。その透徹した論理にひめられた核心が、平明このうえない訳文と懇切丁寧な注釈により明らかになる。主著、待望の新訳。
-
-認知症を恐れないために! 幕末医療漫画『JIN-仁-』の脳外科医・南方仁が認知症研究の第一人者に迫る。認知症と脳の仕組み、VRゴーグルを用いた認知症の「超」早期発見、そして実践したい日々の予防法。認知症は要因と経過を正しく知り、超早期に見つけることができれば、重症になってしまう前に対策を立てられる。そのための鍵となる「VRゴーグルを使った空間ナビゲーション脳機能測定」とは? 『JIN-仁-』の作者・村上もとかの書きおろしイラストを収録。
-
3.0黒船から開国・討幕へ――激動の15年間を、さまざまな立場の11名から読み解くことで、立体的に幕末史が捉えられるようになる1冊。教科書や歴史小説、ドラマから作られた人物イメージが覆る。歴史に名を遺した人々は、何を決断し、どう生きたのか?
-
-
-
3.7
-
5.0※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 「日本の歴史を変えた!」と言えるような、日本史上に残る人物から365人をピックアップして、その功績や人物面について解説。それぞれの人物をより深く知るためにオススメの書籍と、また、特に重要な人物には佐藤優による別角度からのコメントが加えられており、教科書だけでは知ることの出来ない、深い教養が身につきます。ビジネスパーソンなどが最低限身につけておきたい教養を網羅しています。
-
4.02020年は『日本書紀』編纂からちょうど1300年の年に当たります。 最近では、古代史ブームの高まりから、初代とされる神武天皇以降の「初期天皇」、葛城氏をはじめとする古代豪族など、教科書には載っていない3~5世紀の時代への関心も高まり、その歴史的重要性が見直されつつあります。 本書では、登場人物を中心に『日本書紀』を扱うことで、個々の登場人物の魅力や「その後」、ほんとうに敗者だったのか、その後どのように伝承されていったのか、など、『日本書紀』をより楽しめます。 「日本書紀の基礎知識」「初代神武天皇から41代持統天皇までの歴代天皇」「皇子、女性、豪族など個性豊かな登場人物」という3つの柱で、総計で150人以上の人物を収録。 関連図版・地図も挿入し、ふだん古代史に触れていない方にもおすすめです。
-
3.5歴史の本当の面白さと日本史理解の秘訣は、時代を超えて繋がる人物たちの意外な接点にあった! 後醍醐天皇×織田信長、空海×津田梅子、太田道灌×真田幸村――誰もが知る有名人から、ナンバー2や裏方を担った人物まで、様々な事績やエピソードとともに、現代社会にも通じる思想や教訓を紹介。学び直しにも最適! 2017年NHK大河ドラマ「おんな城主 直虎」時代考証者による、新しい日本史講義。 第 1 章 新時代の幕を開けた人物から学ぶ 1 国盗りの極意は『孫子』にあり 【北条早雲・斎藤道三】 2 革命児の発想が歴史をくつがえす【後醍醐天皇・織田信長】 3 古代 2 つのクーデターの謎 【継体天皇・天智天皇】 4 2 人の明暗を分けたものは何か 【西郷隆盛・大久保利通】 第 2 章 たった 1 人で時代を変えた人物から学ぶ 1 語り継がれる英雄伝説の虚と実 【坂上田村麻呂・源義経】 2 外圧を防いだ小国日本のプライド 【聖徳太子・北条時宗】 3 経済力を握った者が勝つ 【藤原秀衡・平清盛】 4 カリスマ性と人心掌握による統治 【武田信玄・上杉謙信】 第 3 章 組織力で時代を変えた人物から学ぶ 1 民衆のエネルギーを軍制に取り込む 【楠木正成・高杉晋作】 2 新時代のシステムづくり 【足利尊氏・豊臣秀吉】 3 議会制民主主義への胎動 【板垣退助・尾崎行雄】 4 教団の団結力の強さ 【ザビエル・本願寺顕如】 ほか、全12章96人
-
-関西が熱い! プロ野球関西ダービーで注目 関西人とはどういう人なのか ◆関西人とは、訛りを残した世界人である。日本書紀、源氏物語も、徒然草、そして風姿花伝、芭蕉も、司馬遼太郎、谷崎潤一郎も関西産、「世界」標準であり、「不易流行」である。 ◆18歳から関西で23年間過ごした著者が、23人の関西人を取り上げ、その本質に迫る。 ▼開高健、長谷川慶太郎、嵐寛寿郎、松下幸之助、南方熊楠、出口王仁三郎、梅棹忠夫、松田道雄、林達夫、淀川長治、横溝正史、福沢諭吉、三木清、栄陽子、谷沢永一、阪本勝、堺屋太一 他 ◆併せて「社長の哲学」「社長の読書」で、古今東西の人物名鑑を展開。 ▼石橋湛山、ケインズ、ドラッカー、チャーチル、世阿彌、アリストテレス、古田織部正、カーネギー 他 ◆さらにプルタルコス『英雄伝』の人間哲学に学ぶ――東に史記、西に英雄伝 ▼アレクサンドロス、カエサル、キケロ、ブルートゥス、クレオパトラ、スパルタクス、プルタルコスと日本 他
-
3.3
-
-※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 自分で自分の答案を評価する! だから、受かる小論文への仕上げ方がわかる! 周りに添削してくれる人がいない…と困っている受験生にピッタリ。 自分だけで小論文学習が可能になる画期的な1冊です! 「本書では、「自分の力で自分の答案を評価する」という点に重点を置いています。 自分の答案を評価する作業を経験している受験生は少ないでしょう。 しかし、実際に自分の答案を第三者のつもりで評価してみると、採点者がどのような観点で答案を見ているかを理解できます。 そして、自分の答案を客観的に見て改善していく訓練になります。 自分の答案を客観的に評価し、採点し、次の問題で生かすプロセスを通じて、自分の文章をよりブラッシュアップできるのです。 それが「合格答案」につながるのです。」 ー「はじめに」より
-
-日本人の精神のふるさとは縄文にある 芸術の域にまで達する土偶文化が花開き、世界に誇る天皇制の源流へと溯れる縄文時代。 日本文化のルーツを探る旅から見えてくる民族の精神とは 考古学の最新の知見を踏まえて古代日本の実相に迫る歴史ロマン! 【目次より】 プロローグ 縄文土偶の芸術性 第一章 神武天皇はもちろん実在した 第二章 大和政権、邪馬台国と卑弥呼 第三章 『古事記』とて「近代の書物」だ 第四章 世界文明のなかの「縄文」 第五章 日本人の精神構造と道徳は縄文時代に確立されていた エピローグ 大和言葉は縄文語が源流 ・縄文人はどこから日本にやって来たか ・環状列石群には、いったいどんな文明があったのか ・縄文土器、土偶の素晴らしさ ・火焔土器はなぜ生まれたか ・『古事記』の前に聖徳太子によって『天皇記』、『国記』の編纂がなされていた ・大和朝廷にとって女王国の併呑など、取るに足らない事案だった ・『古事記』、『日本書紀』が作り話、政治文書だと言い張っていた人々はいま ・太陽信仰は天照大神にあらわれている ・縄文時代、何語を喋り、どんな絵文字を使用していたのだろう ・かな、カタカナの発明は史上最大級 ・神話は随所に息づいている ・縄文という独自の文明が日本にあった ・人類最古のロゼッタストーン、成文法「ハンムラビ法典」。そしてインカ文明と縄文 ・飛鳥の石舞台、秋田のストーンサークルは英国のストーンヘンジに似ている
-
3.7天皇の初代とされる神武天皇は、生没年はもちろん、その実在さえ定かではない。しかし、伝説上の重要人物として、日本の歴史に大きな影響を与え、論争を呼び起こし、時に政治問題となってきた。天皇陵をめぐる近世・近代史の研究者である著者が、「神武天皇陵」の所在地論争と、橿原神宮の創建を軸に、「歴史学の主題」としての神武天皇に迫る。 初代天皇の墓所「神武天皇陵」は、実は江戸時代になるまで定かではなかった。元禄時代の江戸幕府の調査で、奈良・四条村の塚山に「定められた」のである。しかし、当初からこれには異論があり、幕末期には孝明天皇の意思により、その300メートルほど南の「神武田」に改められ、ここが、現在も天皇が参拝を行う神武天皇陵となっている。一方、国学者の本居宣長らは、畝傍山中の丸山を主張して根強い支持を得ており、明治期になっても「疑念」はくすぶり続けた。さらに、水戸学の巨頭・徳川斉昭、寛政の三奇人・蒲生君平、幕末の能吏・川路聖謨、明治大正の文人画家・富岡鉄斎らの見解もみていく。 また、神武天皇を祀る橿原神宮の創建と隆盛に尽力し、のちに決裂した民間勤王家・奥野陣七の生涯や、明治期に「神武天皇祭」に冷徹な目を向けたお雇い外国人にも注目し、「紀元節」から「建国記念の日」へと、現代にいたる「神武天皇」と日本社会をとらえ直す意欲作。 目次 序章 現代の神武天皇 第一章 三ヵ所の神武天皇陵 第二章 幕末動乱と神武天皇陵 第三章 奈良奉行所与力の結論 第四章 文久の修陵 第五章 明治天皇の親祭 第六章 橿原神宮と民間結社 第七章 消えない疑念 終章 紀元節から「建国記念の日」へ
-
3.3
-
-『古事記』や『日本書紀』で語られる神武東征。初代天皇・神武が九州から困難を乗り越え、ヤマト入りする神話だが、実はこの話、史実だったのではないかと思われる遺跡がある。それが纒向(まきむく)遺跡だ。詳細は本文に譲るが、この遺跡では東海・近江、吉備、出雲の土器が多数発見されており、神話にあるように、最初は纒向を長髄彦(ながすねびこ)が、次に饒速日命(にぎはやひのみこと)が治め、最後に神武がやって来たのではないかと、思われるのだ。高天原から降臨した饒速日命とは一体何者なのか? なぜ長髄彦は、天神である饒速日命は受けいれ、天孫である神武天皇は拒絶したのか? 饒速日命は、義弟を殺してまで、なぜ神武天皇に王権を禅譲したのか?不可解な神話に暗示された、ヤマト王権誕生の謎に迫る!
-
-2017年秋の衆議院総選挙の舞台裏で、何が起きていたのか? そのとき世界は? 人類99%を支配した、寡頭権力者たちの次なる工作とは? 日本政界の深層と世界最先端の情報から世界の「今」を浮き彫りにする! ・陰謀、裏切り、策略が渦巻いた2017年解散総選挙。日本政界の裏側を全部公開します! ・北朝鮮問題はすべてパフォーマンス/人工世紀末劇の洗脳を解け! ・特許庁に申請したあった党名「希望の党」 ・ついに「安倍おろし」が開幕した/再燃化する新安倍と反安倍の対立 ・天皇陛下とプーチンの間で交わされた約束とは? ・トランプ来日の目的は1京円の受け取り!? ・ハリケーン被害者のための募金がパパ・ブッシュに渡った ・限りなく内戦状態に近いアメリカ/ついにハリウッドにもメスが入った! ・イラク戦争ではホログラム技術が使われていた ・アメリカのウラン利権をロシアに売って裏ガネを手にしたクリントン ・タブーとされている長寿のための技術公開/我々の死を願う人々がいる ・AIの発展で世界は良くなる? それとも悪くなる? ・“アンダーコントロール“できていない福島問題 ・戦争を起こしたいハザールマフィアと厭戦のアメリカ軍/第3次世界大戦は本当に起きるのか?
-
5.0人類はどのように平和を希求し、その可能性を探ってきたのか。非攻と兼愛を説いた墨子、国際法の父グロティウスの生命尊重、哲学者カントが夢見た永遠平和、軍人作家ユンガーの平和論、原子爆弾を可能にした科学者ハーンの苦悩、日本史のなかの平和志向……。ノンフィクション作家の著者がキュレーターとなり、古今東西、平和実現のための数々の試みをつなぎ合わせ、現代人に求められる“平和道”を提示する。
-
-森を破壊する西洋型文明から、生命の水と森を守る日本型文明へ 日本の環境考古学の権威で環境史観の提唱者による文明論の集大成 いつしか世界は自然を一方的に収奪・搾取し、お金儲けすることが最高だとする経済学に支配され、自然と共生する歴史観・文明史観は古いタイプのものとしてさげすまれてきた。だが、このまま自然収奪・搾取型の文明で突き進んでいけば、人類は西暦2050年頃に危機を迎えることになる。日本人は自然と持続的に生き続ける歴史観・文明史観とライフスタイルを、縄文時代以来とり続けてきた。日本人が大切にしてきた、(1)生命の水の循環を維持し、(2)自然への畏敬の念を持ち、(3)他者の幸せを願い、(4)資源の循環的利用を考える文明社会を構築してこそ、人類はこの美しい地球で千年も万年も生き延びることが可能になるかもしれない。(「本文より要約抜粋」) 【主な内容】 ・地球の王者の食/・年縞に秘められた謎/・地球の大いなる誤算/・イエスの年縞/・中世温暖期の平氏と源氏/・環太平洋文明圏/・コロンビアの熊野古道/・熱帯林は緑の魔境ではない/・サルスベリの花の記憶/みちのくの未来/・森の長城作戦/・環太平洋の災害と文明/・富士山と三保松原が世界文化遺産になった/・ポスト3・11は生命文明の時代/・日本文明のエートスを世界へ
-
4.1地球温暖化や資源の枯渇、小惑星や彗星の衝突、太陽の膨張……。地球がいずれ壊滅的なダメージを受けることは避けられず、人類は生き延びるために宇宙に移住する必要がある。 世界的に高名な理論物理学者で、未来学者としても定評のある著者が、宇宙移住への道を3つのステップで解説する。まずは月や火星に入植し、次に太陽系外の星々への進出を果たし、それと当時に人体の改造や能力の強化を行うというプランだ。 NASAやイーロン・マスク、ジェフ・ベゾスらの挑戦や、AIやスターシップなど最新テクノロジーの進展を追いながら、驚くべき人類の未来を見通す。最高にエキサイティングな科学読み物。
-
-
-
4.0
-
3.0大野和基 / ジェニファー・ダウドナ / デビッド・A・シンクレア / リサ・ランドール / ジョセフ・ヘンリック / ジョナサン・シルバータウン / チャールズ・コケル / マーティン・リース / ジョナサン・B・ロソス1巻880円 (税込)●遺伝子学・宇宙科学・AI……科学は人類を何処へと誘うか? ●最新科学の研究がもたらす「新たな人類の進化」とは? ●8名の科学の権威が語る、ポスト・ヒューマン世界の展望! ピンポイントでゲノム情報を改変する「クリスパー・キャス9」でノーベル化学賞を受賞したジェニファー・ダウドナ氏や、「人生200年時代」の到来をうたうデビッド・A・シンクレア氏など、一昔前ならSFの世界だったような事象が、いま現実の世界で実現されようとしている。しかし、科学の発展がもたらす「人類の新たな進化」には、大きな思想的・哲学的問題が立ちはだかる。古来より不変の自然の理を超え、人為的に達成される進化を、人類はどのように認識すべきか。そもそも、ヒトが現代の「知性のあるヒト」になったのは必然か、偶然か――。世界の科学者8名が語る、これからの進化論と、ポスト・ヒューマン世界の展望。
-
5.0※この商品はタブレットなど大きいディスプレイを備えた端末で読むことに適しています。また、文字だけを拡大することや、文字列のハイライト、検索、辞書の参照、引用などの機能が使用できません。 宇宙旅行がいよいよ現実に! 宇宙に行くために知っておくべきこと、ここにあります 民間の宇宙旅行予約が開始され、宇宙がますます身近になってきたこの頃。 飛行機に乗るのと同じように、遠くない未来には、あなたもロケットに乗り込む日がやってくるかもしれません。 本書は、いつか宇宙に行くときのために知っておきたい、宇宙の基礎知識やロケットのしくみを、写真やイラスト、図解で分かりやすく解説した「宇宙とロケットの入門書」です。 宇宙はどんなところなのか? ロケットはどういう原理で飛んでいるのか? 宇宙へ行ったら、何ができるのか? 宇宙飛行、宇宙滞在、そして他の惑星へ……人類がもっと遠い宇宙へ行くには、何が必要なのか? 「はやぶさ」プロジェクトにも携わり、『宇宙はどこまで行けるか』(中公新書)の著者である東京大学大学院准教授・小泉宏之氏による、いちばん分かりやすい宇宙とロケットの本ができました。
-
5.0
-
3.8
-
-本書は、日本と欧米における視点の違いを考慮しながら、これまで霊長類学が扱ってきた人類進化のテーマと発見をわかりやすく紹介する入門書。野生霊長類のフィールドワークの成果に基づいて人類の進化史の解明を試みた。 はじめに霊長類学の発想とは何かを紹介し、日本と欧米の考え方の違いを解説する。続いて、人類の誕生の舞台になった熱帯雨林と、そこに適応してきた霊長類の進化史を概観し、他の哺乳類と異なる生活史を進化させたサル、類人猿、人類のそれぞれの特徴をまとめた。また、性の進化、オスの子殺しと暴力、和解行動・道具行動や種々のコミュニケーション能力について、それぞれ章を割いて解説した。最後に、霊長類学の知見から描いたヒトの進化について総括し、まだ解明されていない人類進化の謎について述べた。 本書を通して、(霊長類学によって)人類の過去を遡り、現在の人間を見つめなおす視線を養い、その探求の楽しさが味わえるであろう。
-
4.5私たちはいかにしてヒトになったか? 「ダンバー数」で世界的に有名な進化心理学者ロビン・ダンバーの代表作、待望の文庫化。生物学、神経科学、遺伝学…多彩な視点から人類進化の謎に迫る。 サルはいかにしてヒトになったか? 私たちはなぜ木から降りることを決断したのか? 狩猟採集をしながら世界中を旅してきた私たちは、なぜ歩みを止めて定住し、農耕を始めたのか? ほかの人類種が絶滅してゆく中、なぜ私たちホモ・サピエンスだけが生き残ったのか? 「ダンバー数」で世界的に知られ、 人類学のノーベル賞「トマス・ハクスリー記念賞」を受賞した進化心理学者ダンバーが、 生物学、神経科学、遺伝学など多彩な視点から 人類進化の謎を解き明かした不朽の名著、待望の文庫化。 ■ ■ ■ 人類進化の本筋にせまる著作だ。 私たちヒトという生物がどこから来て、どんな生き物なのかを知りたい人々には、是非お勧めしたい。 ――長谷川眞理子(進化生物学者、総合研究大学院大学名誉教授/「解説」より) 圧倒的な面白さ。 ――瀬名秀明(作家、「週刊ダイヤモンド」書評より) 運命を分けた集団形成の差。 ――柄谷行人(哲学者、「朝日新聞」書評より) 何よりも時間のやりくりに着目した視点自体が面白い。 ――森山和道(サイエンスライター「日経サイエンス」書評より)
-
-
-
-私たちの祖先はどこからきて、どのような暮らしをしていたのか。はたまた、いかにして日本という国をつくるに至ったか──。誰もが一度は考える疑問だが、歴史の教科書にはその答えが十分に載っていない。そこで本書では、約700万年前にアフリカで誕生した人類(猿人)がホモ・サピエンスに進化し、やがて日本列島にたどり着いて統一国家をつくるまでの歩みを一挙解説。氷河に覆われアジア大陸とつながっていた古代日本人類到達以前の日本列島は大型草食動物の天国だった我々の祖先はナウマンゾウとシカを求めて日本列島へ渡った縄文人は舟に乗って貿易を行っていた!弥生人にとってコメは憧れの高級食材だった卑弥呼はじつは外交上手だった!?3世紀から5世紀にかけて古墳群が畿内を転々とした意味4世紀に朝鮮出兵が行われた理由教科書にはほとんど載っていない、旧石器・縄文・弥生・古墳時代の歴史・生活・文化が1冊でまるわかり!
-
3.9フィクションの世界でよく題材にされ,人々の間でイメージが出来上がっている人工冬眠.2020年に発表された著者らの研究成果は,いまだ確立されていないこの技術の実現に向けて飛躍的な貢献をすると期待されている.日々研究開発に挑む研究者としての自身の体験や想いをふんだんに交えながら,「人類冬眠計画」を披露する.
-
3.0ヒトが免疫を獲得していない未知の病原体が、 突如として現れ人間社会を襲うようになった21世紀。 コロナウイルスに限らず、新興感染症の波が次々と襲ってくるのはなぜなのか。 獣医師、疫学者として世界の人獣共通感染症の最前線に立ち続けた著者が、 感染症の培養器となっている工場型畜産から、 感染症を運ぶエキゾチックなペット問題まで、 グローバル化した人間社会が構造的に生み出す 新興感染症とその対応を平易・冷静に描く。
-
4.5
-
3.014万部超えのベストセラー『中国の大問題』に続く、丹羽宇一郎氏のPHP新書第2弾。1972年に刊行されたベストセラー『成長の限界』は、「あと20年で石油は枯渇し、人類の成長は限界に達する」と警鐘を鳴らし、世界を震撼させた。結果的に、その予測は現実のものとはならなかったものの、あれから40年以上経ち、地球の人口は倍増し、温暖化も進み、食料や水の枯渇リスクも高まってきた。たしかに最近、日本でも頻発する集中豪雨や巨大化する台風などの“地球の反乱”には、私たちの想像をはるかに超えるものがある。にもかかわらず、「なんとかなるさ」と知らん顔を決め込んでいる人間は、傲慢すぎるのでは――。昨冬のCOP21では、世界196の国・地域が温暖化に対する取り組みで合意に達したが、いまこそ、人類の英知が試されるときである。著者が自らの商社マン時代、中国大使時代の体験も踏まえ、人類の未来を展望し、真の安全保障を考える一冊。
-
4.0